本文介绍权重初始化
权重初始化
预备知识
期望的性质
$$E(C) = C \tag{1}$$
$$E(aX) = aE(X) \tag{2}$$
$$E(X+Y) = E(X)+E(Y) \tag{3}$$
$$E(\sum_{i=1}^{n}a_iX_i+C) = \sum_{i=1}^{n}a_iE(X_i)+C \tag{4}$$
当$X$和$Y$相互独立时，
$$E(XY) = E(X)E(Y) \tag{5}$$
方差的性质
$$
D(X) = E((X-E(X))^2) \
= E(X^2-2E(X)X+E^2(X)) \
= E(X^2)-2E^2(X)+E^2(X) \
= E(X^2)-E^2(X) \tag{6}
$$
$$D(X) \not< 0 \tag{7}$$
$$D(C) = 0 \tag{8}$$
$$D(CX) = C^2D(X) \tag{9}$$
$$D(aX+bY) = a^2D(X)+b^2D(Y)+2abE(X-E(X))(Y-E(Y))$$
如果$X$，$Y$相互独立，则
$$D(aX+bY) = a^2D(X)+b^2D(Y) \tag{10}$$
如果$X$，$Y$相互独立，且$E(X)=E(Y)=0$，由$式(6)$和$式(5)$，
$$
D(XY) = E((XY-E(XY))^2) \
= E(X^2Y^2)-E^2(XY) \
= E(X^2)E(Y^2)-E^2(X)E^2(Y) \
= E(X^2)E(Y^2) \
= E((X-E(X))^2)E((Y-E(Y))^2) \
= D(X)D(Y) \tag{11}
$$
为何初始化
神经网络使用误差反向传播算法（梯度下降）来训练，其需要从输出向输入逐层求导，根据导数（梯度）来更新权重，然后继续下一轮迭代。如果求出的导数（梯度）过小，那么权重的更新幅度会很小，学习速度就会变慢，甚至无法收敛。
训练之前需要给神经网络的权重赋初始值，初始值的选择会对导数有很大影响。
以神经网络中常用的激活函数sigmoid函数为例，如图，当函数的输入值的绝对值越来越大时，函数值越来越平滑，趋于饱和，梯度趋于0。如果把输入值限制在$[-2,2]$区间，sigmoid函数可以获得较大的梯度。神经网络的结构是线性变换层然后到激活层，这就要求线性变换层的输出值在$[-2,2]$区间。通过给权重赋恰当的初始值，可以使线性变换输出值在较理想的范围内。
假设$z$为神经网络层线性变换的输出结果，$w$为该层参数，$x$为该层输入，
$$z = \sum_{i=1}^nw_ix_i+b$$
假设输入数据中每一维都是相互独立的，根据$公式(3)$、$公式(10)$和$公式(11)$，$z$的方差为
$$
D(z) = D(\sum_{i=1}^{n}w_ix_i) \
= \sum_{i=1}^nD(w_ix_i) \
= nD(w_ix_i) \
= nD(w_i)D(x_i) \tag{12}
$$
若输入层有1000个神经元，隐藏层有1个神经元，输入数据$x$是1000维的全1向量。使用标准正态分布（均值为0，方差为1）来初始化权重矩阵$w$，偏执初始化为0，则输出$z$服从均值为0，方差为1000的正态分布。
由此可见，数据经过线性变换之后，方差被放大了数倍（放大的倍数与输入的维度相关），输出绝对值远大于1的概率也增大了，再经过sigmoid激活，就有可能使sigmoid饱和，梯度变得很小，权重更新变得缓慢。
几种初始化方式
全零初始化
将所有参数都初始化为0，这时线性变换的输出的期望能达到理想状态。但是参数全0时不同神经元的输出相同，各神经元的梯度也完全一样，这将导致更新后的参数仍然保持一样的状态，神经网络将无法训练。所以全零初始化不可行。
随机初始化
简单的随机初始化（正态分布或者均匀分布）会遇到输入经线性变换后的方差增大的问题，如上所述。
Xavier初始化
Xavier初始化的基本思想是保持输出的方差和输入一致，这样可以避免激活后所有的输出值趋向于0。
可以使用均值为0、方差为1的随机变量初始化权重，即$D(w_i)=1$，但是由于线性变换输出的方差会随着神经元个数改变，所以需要加上对方差大小的规范化，具体做法是在随机初始化的基础上乘以规范化系数$\frac{1}{\sqrt n}$，其中$n$是输入神经元个数。根据$公式(10)$有
$$
D(z) = D(\sum_{i=1}^{n}\frac{1}{\sqrt n}w_ix_i) \
= \sum_{i=1}^n(\frac{1}{\sqrt n})^2D(w_ix_i) \
= D(w_ix_i) \
= D(w_i)D(x_i) \
= D(x_i)
$$
等价的也可以使用均值为0，方差为$\frac{1}{n}$的随机变量来初始化权重，即$D(w_i)=\frac{1}{n}$，根据$公式(12)$有
$$D(z) = nD(w_i)D(x_i) = D(x_i)$$
但是还有考虑反向传播的场景，反向传播是正向传播的逆过程，此时的输入是前向传播的输出，所以应该令
$$D(w_i)=\frac{1}{n_{in}+n_{out}}$$
Xavier初始化适用于激活函数是sigmoid和tanh。使用的分布可以是正态分布或者均匀分布。
He初始化
Xavier初始化没有考虑非线性映射对下一层输入的影响，比如使用Relu激活函数之后，输出的期望往往不是0。He初始化提出了改进方法：将非线性映射造成的影响考虑进参数初始化中，它提出方差规范化系数应该是$\sqrt \frac{2}{n}$而不是$\frac{1}{\sqrt n}$。
He初始化适用于激活函数是Relu。使用的分布可以是正态分布或者均匀分布。
BN
BN层将输入数据分布变成标准正态分布（规范化），这样可以保证每一层神经网络的输入保持相同分布。它可以削弱不恰当的参数初始化造成的影响，使参数初始化不依赖于神经元个数。有BN层时，参数初始化可以使用随机初始化方式。
Tensorflow2.0中的权重初始化函数
lecun初始化（正态分布）
tf.initializers.lecun_normal函数。
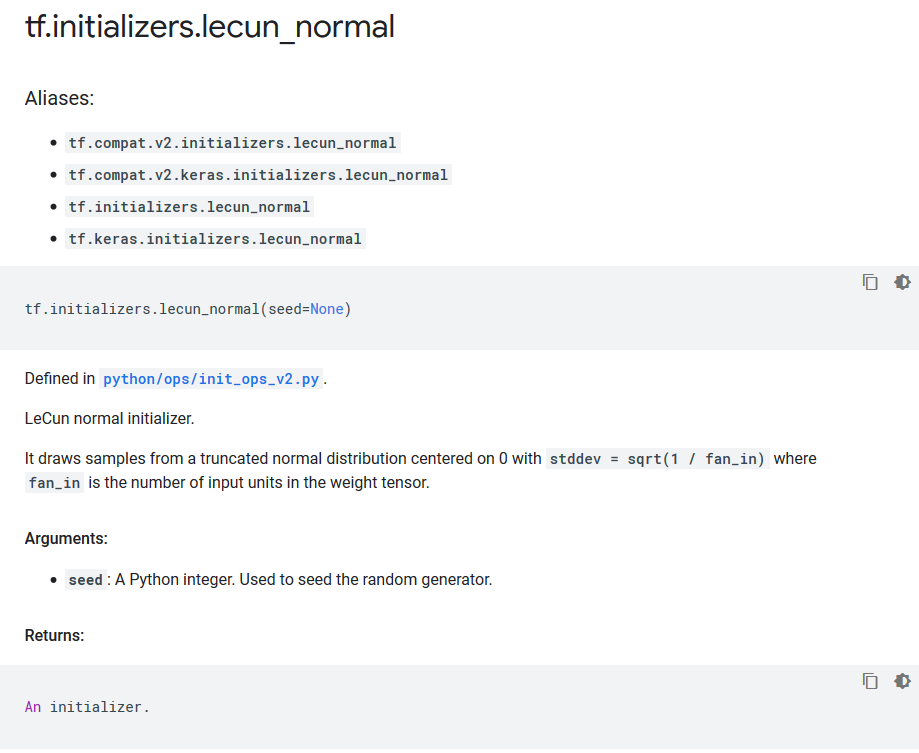
从方差为$\sqrt \frac{1}{n_{in}}$的截断正态分布中采样，得到权重初始化值。
lecun初始化（均匀分布）
tf.initializers.lecun_uniform函数。
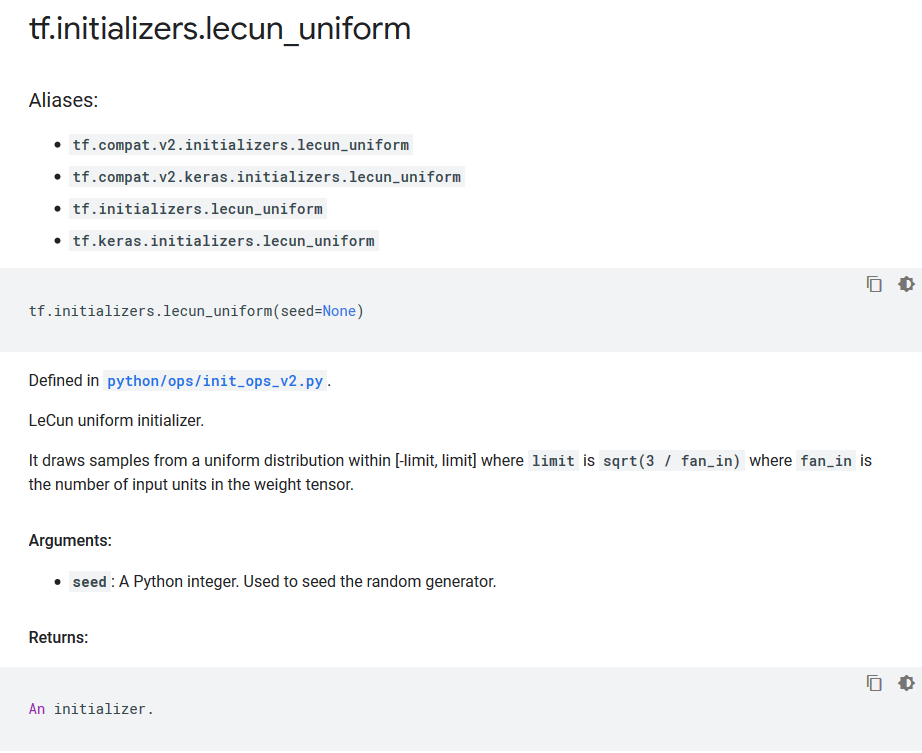
从$[-\sqrt \frac{3}{n_{in}} , \sqrt \frac{3}{n_{in}}]$的均匀分布中中采样，得到权重初始化值。
Xavier初始化（正态分布）
也叫Glorot初始化。
tf.initializers.GlorotNormal类。
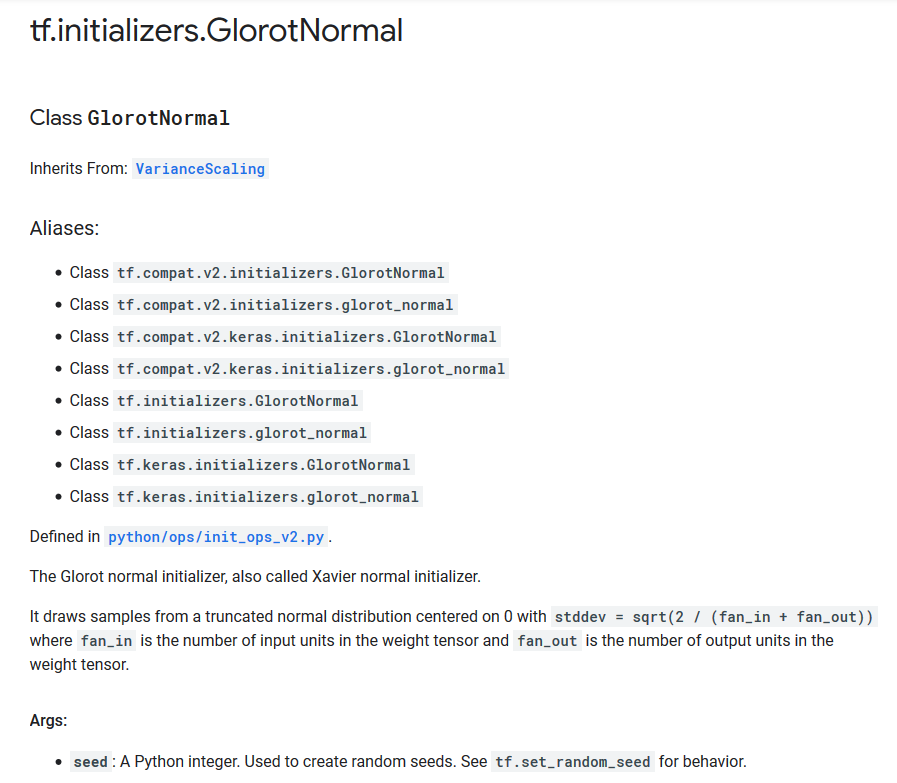
从方差为$\sqrt \frac{2}{n_{in}+n_{out}}$的截断正态分布中采样，得到权重初始化值。
Xavier初始化（均匀分布）
tf.initializers.GlorotUniform类。
从$[-\sqrt \frac{6}{n_{in}+n_{out}} , \sqrt \frac{6}{n_{in}+n_{out}}]$的均匀分布中中采样，得到权重初始化值。
He初始化（正态分布）
tf.initializers.he_normal函数。
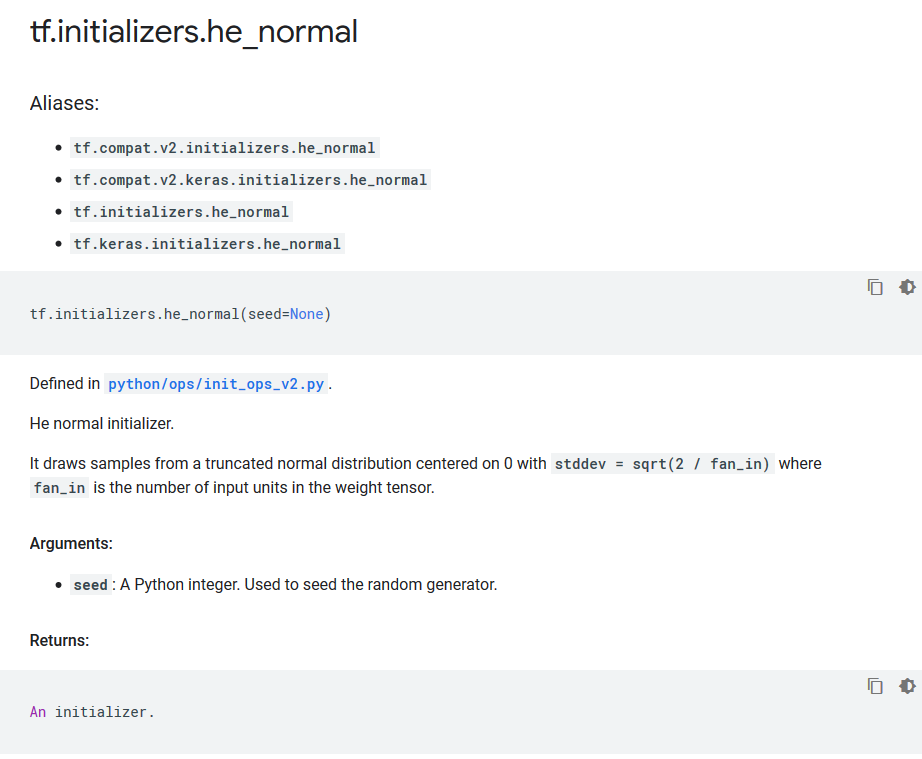
从方差为$\sqrt \frac{2}{n_{in}}$的截断正态分布中采样，得到权重初始化值。
He初始化（均匀分布）
tf.initializers.he_uniform函数。
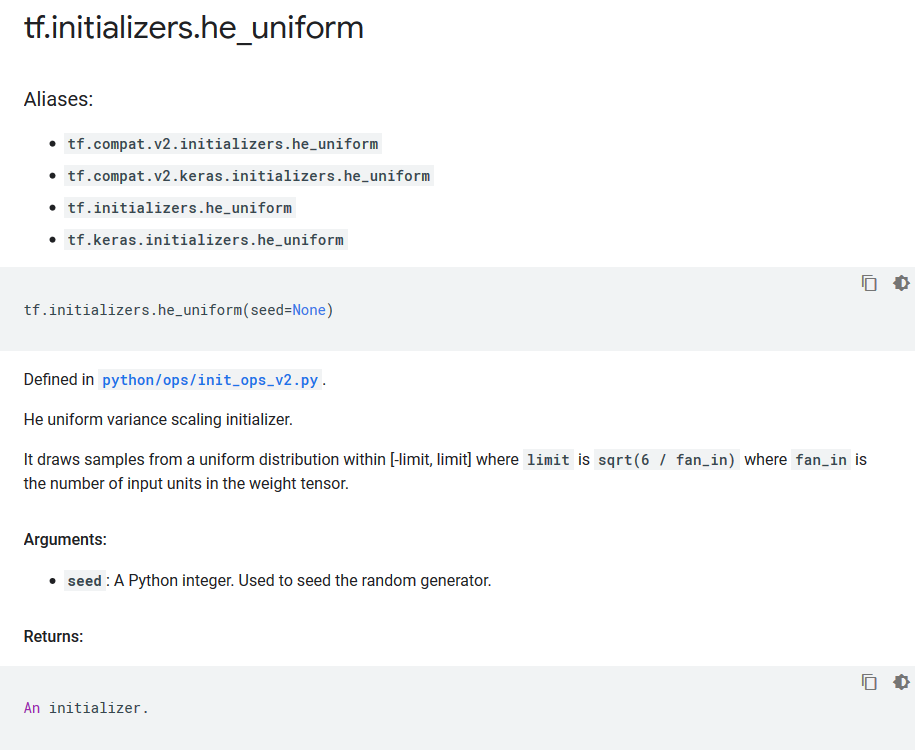
从$[-\sqrt \frac{6}{n_{in}} , \sqrt \frac{6}{n_{in}}]$的均匀分布中中采样，得到权重初始化值。
Pytorch中的权重初始化
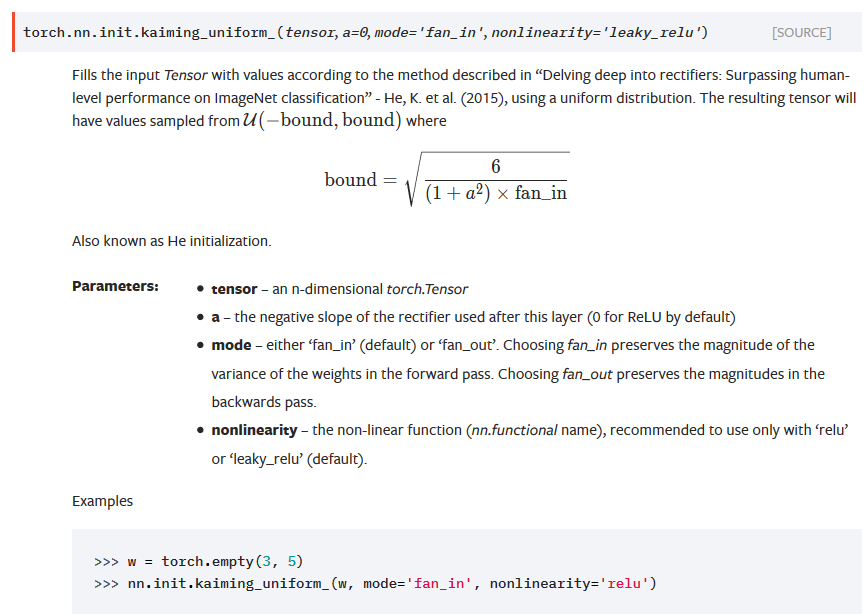
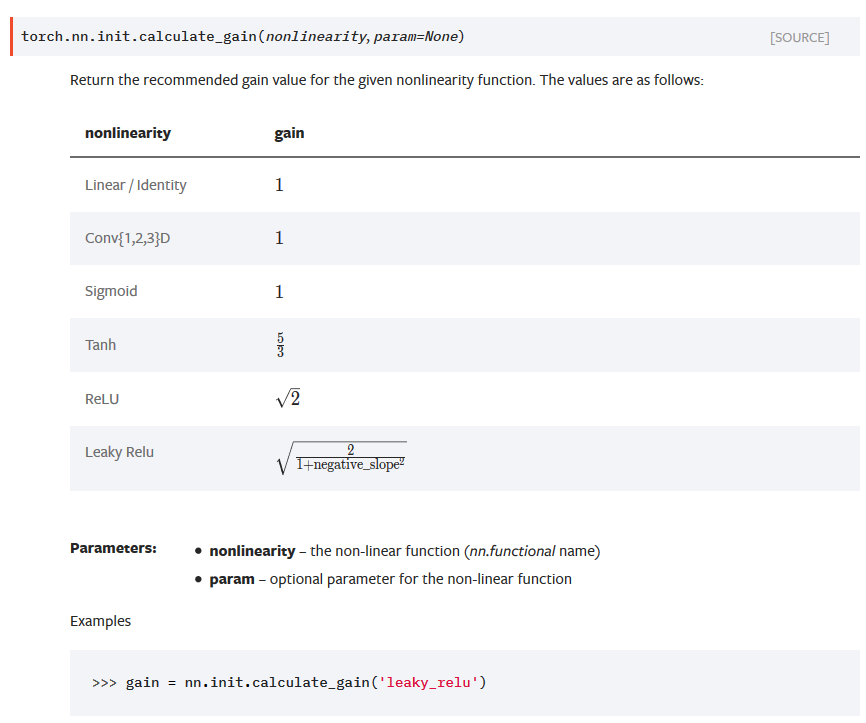
torch.nn.init.calculate_gain函数根据非线性函数来计算出权重初始化系数，后面会用到。
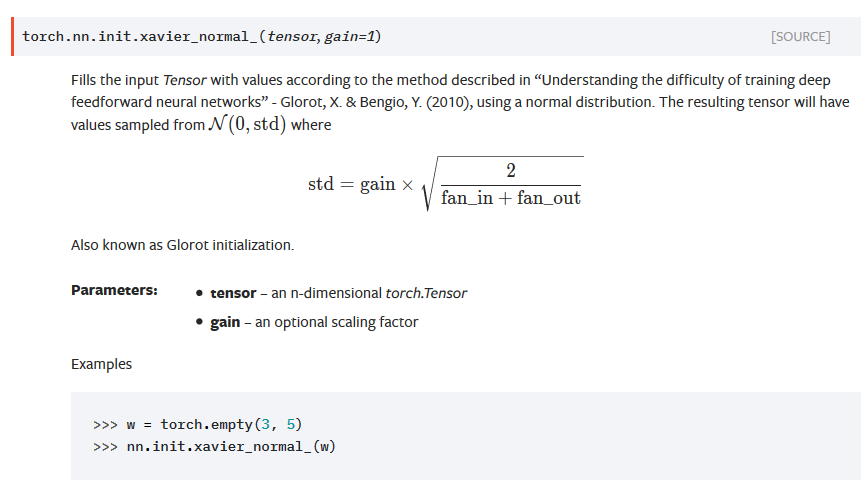
Xavier初始化（正态分布）
torch.nn.init.xavier_normal_函数。
Xavier初始化（均匀分布）
torch.nn.init.xavier_uniform_函数。
He初始化（正态分布）
torch.nn.init.kaiming_normal_函数。
He初始化（均匀分布）
torch.nn.init.kaiming_uniform_函数。
